Groundsense

An Exploration of Gradient Lattice for Personalized Midsole Performance

2025

Keywords
Footwear Design
Gradient Lattice
FEA and Optimization
Tools
Rhino Grasshopper (Millipede, Opossum)
C# Scripting
Keyshot
highlights
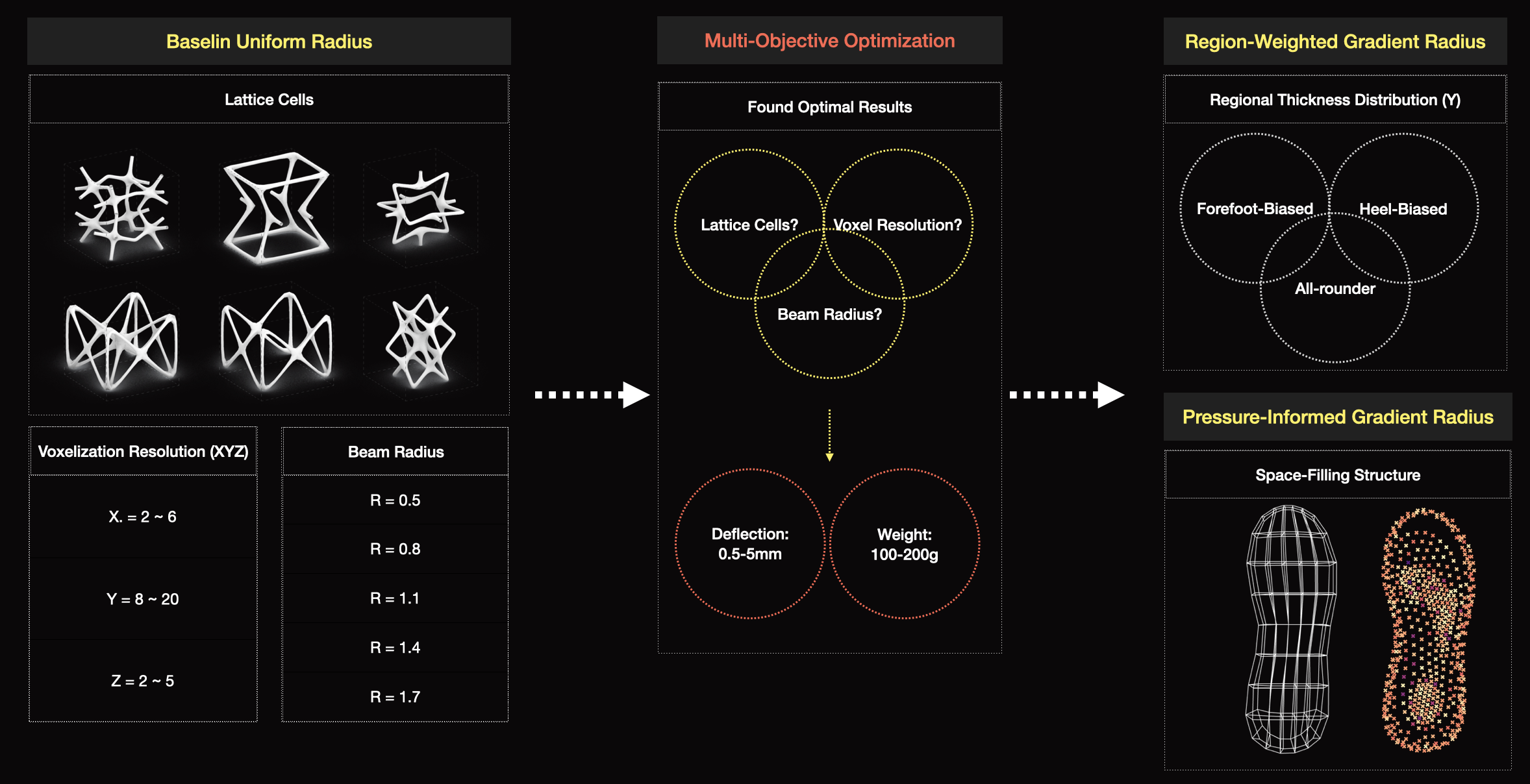
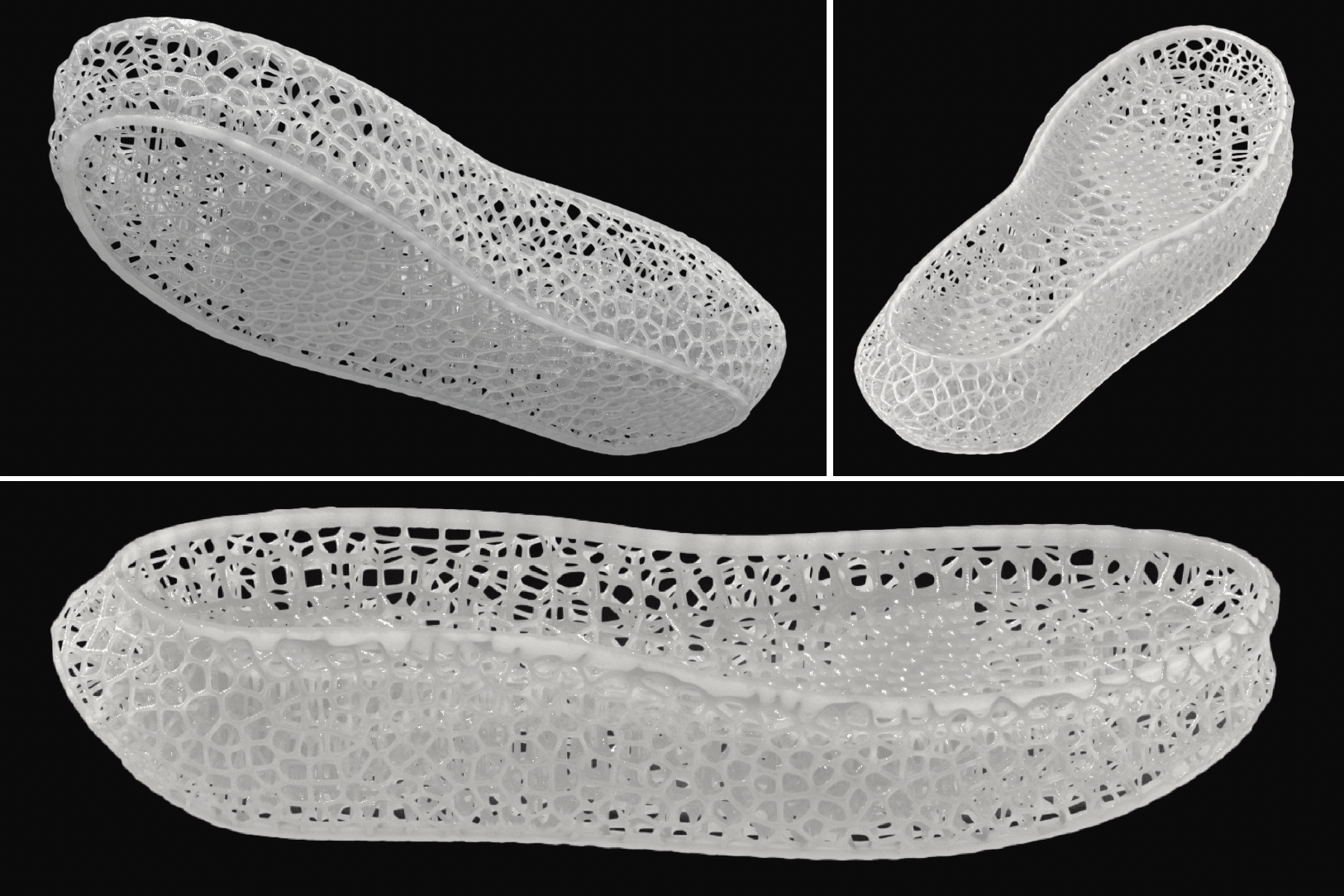
Intuition v.s. Data: Two gradient strategies—designer-intuition zoning and pressure-map-informed adaptation—reveal where design assumptions align with or diverge from biomechanical reality.

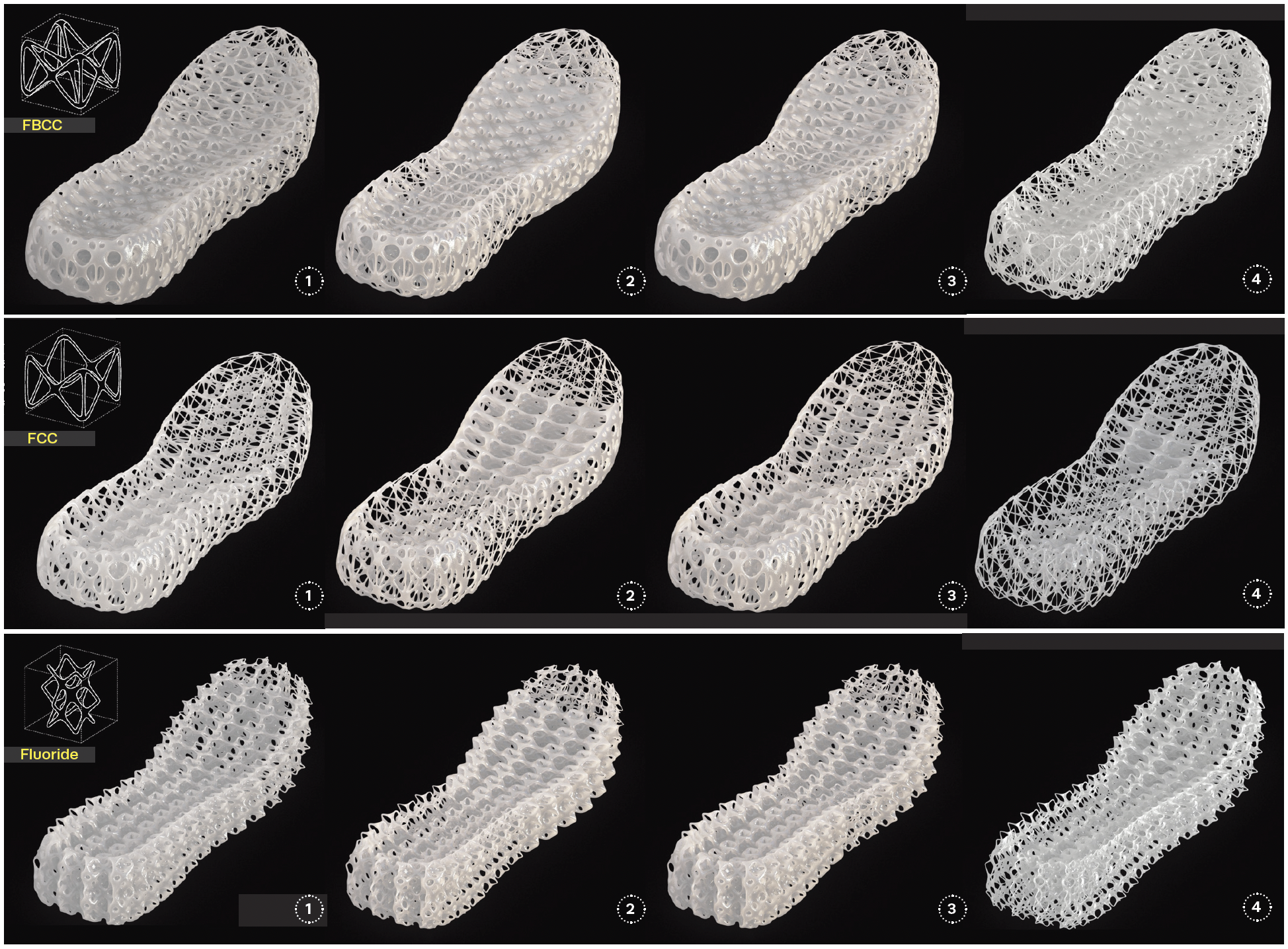
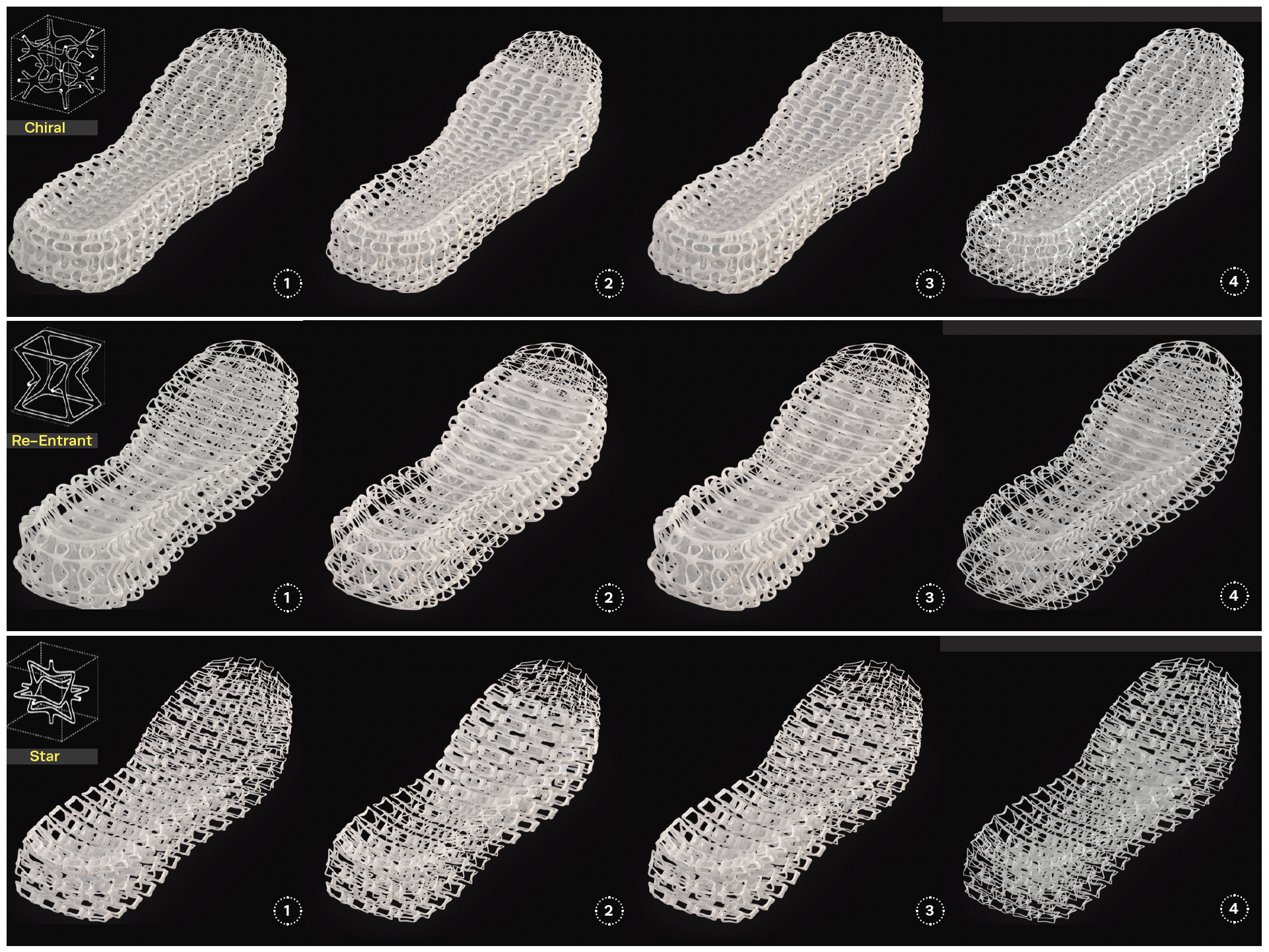
Micro-to-Macro Performance: How do lattice beam morphologies at millimeter scale influence cushioning, weight and stability at the shoe level? Six lattice typologies provide answers.
about
Traditional midsoles use uniform foam density, but our feet don’t load uniformly. This project explores computational lattice structures for performance footwear that integrate lattice geometry, data-driven stiffness gradients, and human-centered performance tuning.
‍
By evaluating six lattice typologies and two material gradient approaches, the work reveals how micro-scale lattice morphology influences macro-scale comfort, stability, and weight —informing design decisions for different athletic applications.
‍
Workflow
The process starts from the lattice topology generation and material gradient distribution-- six lattice structures are generated through discrete voxelization, followed by two gradient approaches. This establishes the design space of structural patterns and variable beam radii before optimization.

Then the finite element analysis with Millipede and multi-objective optimization with Opossum were exercised to assess comfort-performance balance for each lattice topology and gradient configuration. The results guide the selection of high-performing lattice candidates and validate how geometry topology and material gradient distribution influence overall performance.
‍
Unit lattice

Six unit lattice geometries, including 3 auxetic geometry(Chiral, Re-entrant, Star) and 3 structural geometry (FBCC, FCC and Fluoride), were generated and applied to the midsole area.

Gradient Lattice
Two gradient approaches were explored:
1) Design intuition meets biomechanics: beam thickness increases with expected load performance
- Toe 0.7mm (Flexible and Printable)
- Forefoot 1mm (Propulsion)
- Arch 1.3mm (Support)
- Heel 1.6mm (Impact absorption)

2) Pressure data informed: the more load, the thicker of the beam

Finite Element Analysis
A uniform-radius lattice was used as a baseline to evaluate how topology, voxel resolution, and beam radius affect midsole performance. Millipede and Opossum plugins evaluated deflection and weight across all candidates.
‍
Key findings:
1) Re-entrant lattices consistently achieve the best comfort–weight tradeoff.
2) 0.8–1.4 mm beam radii provide stable, printable structures.
3) Lower X/Z voxel densities reduce over-stiff regions and improve compliance.
‍
These results establish the parameter range used for the subsequent gradient-thickness studies.
‍
The optimal parameters were then applied to the lattice structures that using gradient beam radii
‍
Key findings:
1) Regional gradients:
- Forefoot-biased & All-rounder = softest/lightest;
- Heel-biased = stiffest/heaviest;
‍
2) Data-driven gradients: Always achieve better comfort–weight balance than intuition or uniform radius.
‍
3) Structure effect: Voxel lattices outperform Voronoi for cushioning and targeted stiffness.
‍